Southward.2 Confidence Intervals

Let'southward review the basic concept of a conviction interval.

Suppose we want to estimate an bodily population mean \(\mu\). Equally you know, we can only obtain \(\bar{x}\), the hateful of a sample randomly selected from the population of interest. We can use \(\bar{x}\) to find a range of values:

\[\text{Lower value} < \text{population hateful}\;\; \mu < \text{Upper value}\]

that we can be really confident contains the population mean \(\mu\). The range of values is called a "conviction interval."

Example S.2.one

Should using a manus-held cell phone while driving exist illegal? Department

There is trivial incertitude that over the years yous accept seen numerous confidence intervals for population proportions reported in newspapers.

For example, a newspaper report (ABC News poll, May 16-20, 2001) was concerned whether or non U.S. adults thought using a paw-held jail cell telephone while driving should be illegal. Of the one,027 U.S. adults randomly selected for participation in the poll, 69% thought that it should be illegal. The reporter claimed that the poll's "margin of error" was 3%. Therefore, the confidence interval for the (unknown) population proportion p is 69% ± 3%. That is, we tin can be really confident that betwixt 66% and 72% of all U.S. adults think using a hand-held cell phone while driving a machine should be illegal.

General Class of (Near) Confidence Intervals Section

The previous instance illustrates the general form of near confidence intervals, namely:

$\text{Sample estimate} \pm \text{margin of fault}$

The lower limit is obtained by:

$\text{the lower limit L of the interval} = \text{estimate} - \text{margin of error}$

The upper limit is obtained by:

$\text{the upper limit U of the interval} = \text{approximate} + \text{margin of error}$

In one case we've obtained the interval, we tin claim that nosotros are really confident that the value of the population parameter is somewhere between the value of L and the value of U.

And then far, we've been very general in our discussion of the calculation and interpretation of confidence intervals. To be more than specific nigh their utilise, let'due south consider a specific interval, namely the " t-interval for a population hateful µ ."

(1-α)100% t-interval for the population mean \(\mu\)

If we are interested in estimating a population mean \(\mu\), it is very probable that we would apply the t-interval for a population mean \(\mu\).

t-Interval for a Population Mean
The formula for the confidence interval in words is:

$\text{Sample mean} \pm (\text{t-multiplier} \times \text{standard error})$

and y'all might remember that the formula for the confidence interval in annotation is:
$\bar{x}\pm t_{\alpha/2, due north-1}\left(\dfrac{southward}{\sqrt{due north}}\correct)$

Note that:

  • the " t-multiplier," which we announce equally \(t_{\alpha/ii, north-1}\), depends on the sample size through n - ane (called the "degrees of freedom") and the confidence level \((1-\blastoff)\times100%\) through \(\frac{\blastoff}{2}\).
  • the "standard error," which is \(\frac{s}{\sqrt{n}}\), quantifies how much the sample means \(\bar{x}\) vary from sample to sample. That is, the standard error is just another proper noun for the estimated standard deviation of all the possible sample ways.
  • the quantity to the right of the ± sign, i.e., " t -multiplier × standard error," is just a more specific form of the margin of error. That is, the margin of error in estimating a population mean µ is calculated by multiplying the t-multiplier by the standard error of the sample mean.
  • the formula is simply appropriate if a sure assumption is met, namely that the data are normally distributed.

Conspicuously, the sample hateful \(\bar{x}\) , the sample standard divergence due south, and the sample size due north are all readily obtained from the sample data. Now, we but need to review how to obtain the value of the t-multiplier, and nosotros'll be all set.

How is the t-multiplier adamant?

As the post-obit graph illustrates, we put the conviction level $i-\blastoff$ in the middle of the t-distribution. Then, since the entire probability represented by the curve must equal i, a probability of α must exist shared every bit among the ii "tails" of the distribution. That is, the probability of the left tail is $\frac{\alpha}{2}$ and the probability of the right tail is $\frac{\alpha}{2}$. If we add up the probabilities of the various parts $(\frac{\alpha}{2} + one-\alpha + \frac{\alpha}{ii})$, we get 1. The t-multiplier, denoted \(t_{\blastoff/two}\), is the t-value such that the probability "to the right of it" is $\frac{\alpha}{two}$:

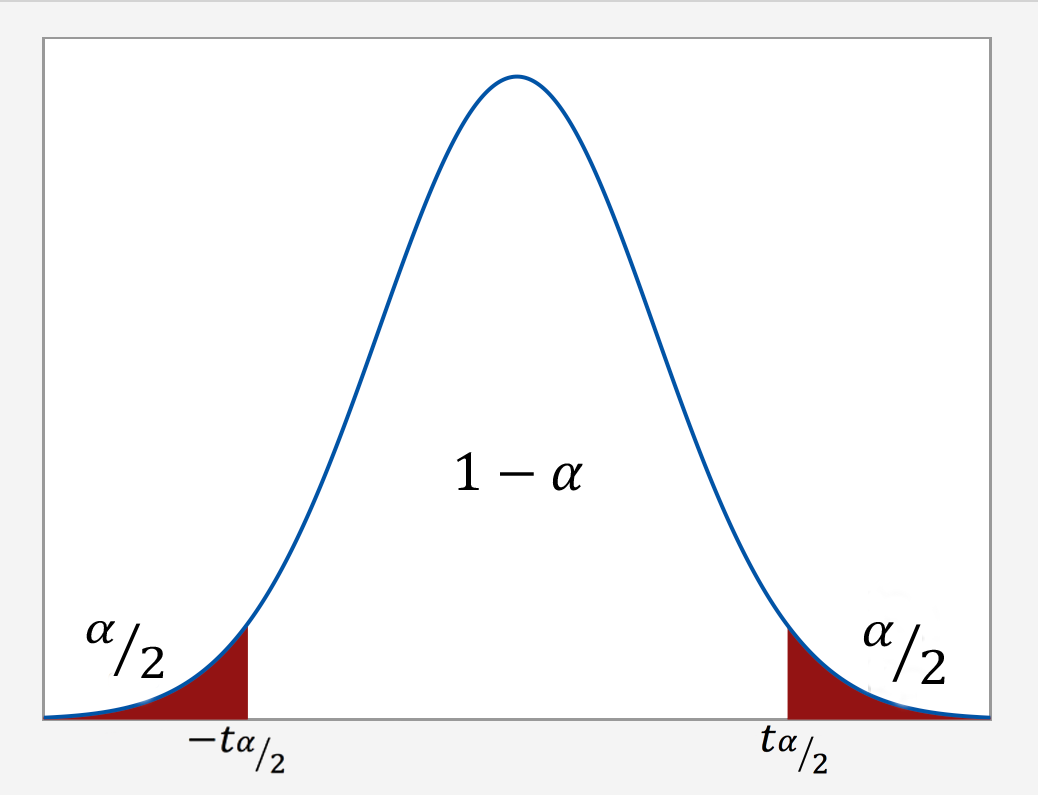
t-distribution

It should be no surprise that nosotros desire to exist equally confident as possible when we estimate a population parameter. This is why confidence levels are typically very loftier. The nigh mutual conviction levels are 90%, 95% and 99%. The post-obit table contains a summary of the values of \(\frac{\alpha}{2}\) corresponding to these common conviction levels. (Note that the"confidence coefficient" is just the confidence level reported every bit a proportion rather than as a percentage.)

Confidence levels
Confidence Coefficient $(1-\alpha)$ Confidence Level $(i-\alpha) \times 100$ $(1-\dfrac{\blastoff}{ii})$ $\dfrac{\blastoff}{2}$
0.90 90% 0.95 0.05
0.95 95% 0.975 0.025
0.99 99% 0.995 0.005

Minitab 18

Minitab®  – Using Software

The adept news is that statistical software, such as Minitab, will calculate most confidence intervals for the states.

Let'due south take an case of researchers who are interested in the average heart rate of male person college students. Presume a random sample of 130 male person higher students were taken for the study.

The following is the Minitab Output of a i-sample t-interval output using this information.

One-Sample T: Heart Charge per unit

Descriptive Statistics
N Hateful StDev SE Mean 95% CI for $\mu$
130 73.762 7.062 0.619 (72.536, 74.987)

$\mu$: mean of Hour

In this instance, the researchers were interested in estimating \(\mu\), the heart rate. The output indicates that the mean for the sample of n = 130 male students  equals 73.762. The sample standard deviation (StDev) is 7.062 and the estimated standard error of the mean (SE Mean) is 0.619. The 95% conviction interval for the population mean $\mu$ is (72.536, 74.987). We can be 95% confident that the hateful centre charge per unit of all male college students is between 72.536 and 74.987 beats per minute.

Factors Affecting the Width of the t-interval for the Hateful $\mu$ Department

Call back virtually the width of the interval in the previous case. In general, do you think nosotros desire narrow conviction intervals or wide confidence intervals? If you are not certain, consider the following two intervals:

  • We are 95% confident that the average GPA of all higher students is betwixt one.0 and 4.0.
  • We are 95% confident that the average GPA of all higher students is betwixt 2.7 and 2.nine.

Which of these two intervals is more than informative? Of course, the narrower one gives us a better idea of the magnitude of the true unknown boilerplate GPA. In full general, the narrower the confidence interval, the more information we take almost the value of the population parameter. Therefore, we want all of our confidence intervals to be equally narrow equally possible. So, let's investigate what factors affect the width of the t-interval for the mean \(\mu\).

Of course, to find the width of the conviction interval, nosotros just take the difference in the ii limits:

Width = Upper Limit - Lower Limit

What factors affect the width of the conviction interval? We tin can examine this question by using the formula for the confidence interval and seeing what would happen should one of the elements of the formula exist allowed to vary.

\[\bar{x}\pm t_{\blastoff/2, n-1}\left(\dfrac{s}{\sqrt{n}}\correct)\]

What is the width of the t-interval for the hateful? If you subtract the lower limit from the upper limit, y'all get:

\[\text{Width }=ii \times t_{\alpha/2, n-i}\left(\dfrac{s}{\sqrt{n}}\correct)\]

Now, allow's investigate the factors that affect the length of this interval. Convince yourself that each of the following statements is accurate:

  • As the sample mean increases, the length stays the same. That is, the sample mean plays no office in the width of the interval.
  • As the sample standard deviation due south decreases, the width of the interval decreases. Since southward is an gauge of how much the information vary naturally, we take little control over s other than making sure that we brand our measurements as carefully as possible.
  • As nosotros decrease the confidence level, the t-multiplier decreases, and hence the width of the interval decreases. In practice, we wouldn't desire to set the confidence level below 90%.
  • As nosotros increase the sample size, the width of the interval decreases. This is the cistron that we accept the nearly flexibility in changing, the only limitation being our time and financial constraints.

In Closing

In our review of confidence intervals, we have focused on merely one confidence interval. The of import thing to recognize is that the topics discussed here — the full general course of intervals, determination of t-multipliers, and factors affecting the width of an interval — by and large extend to all of the conviction intervals we volition encounter in this course.